tech

Range Sum Query

Range Sum Query, 对一个整数序列，给定范围对其求和。根据序列的维度可分为一维、二维和多维，根据元素是否可以改变分为Immutable和Mutable，我们只讨论一维和二维的情况。

1. 1D, Immutable（一维，数据不可变）

Given an integer array nums, find the sum of the elements between indices i and j (i ≤ j), inclusive.

Example:
Given nums = [-2, 0, 3, -5, 2, -1]

sumRange(0, 2) -> 1
sumRange(2, 5) -> -1
sumRange(0, 5) -> -3
Note:

  1. You may assume that the array does not change.
  2. There are many calls to sumRange function.

Analysis

如果采取brute-force, 在每次query的时候，则需要用O(n)的时间复杂度计算sumRange(i, j)，整个时间复杂度就为O(n^2),这样做必然是会超时，因此这种方法不可行。

这种方法在每次query的时候都需要将i到j的元素累加，比如第一次query的是(0,2)，第二次query的是(0,3), 我们可以发现第二次的计算是可以利用第一次的结果的。因此可以对算法进行改进，在一开始进行适当的计算，并保存结果，在增加空间复杂度的前提下减小时间复杂度。最后在query的时候就可以节省大量时间了，那么关键是我们要保存什么信息呢？
可以发现：

1
sumRange(i, j) = sumRange(0, j) - sumRange(0, i-1)

假如我们已经计算了每个sumRange(0, k),那么我们既可以在O(1)的算法时间复杂度内完成query。计算所有的sumRange(0, k)可以利用动态规划，O(n)的时间即可完成。因此整个算法的时间复杂度为O(n)，空间复杂度也为O(n)。

Cpp Code

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
class NumArray {
public:
    NumArray(vector<int> &nums) {
        int n = nums.size();
        cusums.resize(n+1, 0);  // cusums[0]=0
        for(int i = 1; i <= n; i++)
            cusums[i] += cusums[i-1] + nums[i-1];
    }
    int sumRange(int i, int j) {
        return cusums[j+1]-cusums[i];
    }   
private:
    vector<int> cusums;
};

// Your NumArray object will be instantiated and called as such:
// NumArray numArray(nums);
// numArray.sumRange(0, 1);
// numArray.sumRange(1, 2);

2. 2D, Immutable（二维，数据不可变）

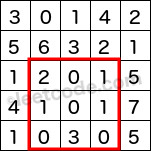
Given a 2D matrix matrix, find the sum of the elements inside the rectangle defined by its upper left corner (row1, col1) and lower right corner (row2, col2).
Range Sum Query 2D
The above rectangle (with the red border) is defined by (row1, col1) = (2, 1) and (row2, col2) = (4, 3), which contains sum = 8.

Example:
Given matrix = [
[3, 0, 1, 4, 2],
[5, 6, 3, 2, 1],
[1, 2, 0, 1, 5],
[4, 1, 0, 1, 7],
[1, 0, 3, 0, 5]
]
sumRegion(2, 1, 4, 3) -> 8
sumRegion(1, 1, 2, 2) -> 11
sumRegion(1, 2, 2, 4) -> 12
Note:
You may assume that the matrix does not change.
There are many calls to sumRegion function.
You may assume that row1 ≤ row2 and col1 ≤ col2.

Analysis

与1维的处理方法相同，只不过二维的情形需要O(n^2)的时间预处理。主要利用一下公式：

1
2
3
4
sumRegion(row1, col1, row2, col2) = 
                          sumRegion(0, 0, row2, col1)
                        + sumRegion(0, 0, row1, col2)
                        - sumRegion(0, 0, row1, col1)

在实际处理中，定义积分图矩阵integrogram的第一行和第一列为0,方便使用统一公式处理，不用讨论为0的情况。

Cpp Code

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
class NumMatrix {
public:
    NumMatrix(vector<vector<int>> &matrix) {
        n = matrix.size();
        m = n != 0 ? matrix[0].size() : 0;
        integrogram.resize(n+1, vector<int>(m+1, 0));  // 第一行，第一列为0
        for(int i = 1; i <= n; i++)
        {
            for(int j = 1; j <= m; j++)
            {
                integrogram[i][j] = integrogram[i-1][j] 
                                  + integrogram[i][j-1] 
                                  - integrogram[i-1][j-1]
                                  + matrix[i-1][j-1];
            }
        }
    }

    int sumRegion(int row1, int col1, int row2, int col2) {
        if(row1 < 0 || col1 < 0 || row2 > n || col2 > m)
            return 0;
        return integrogram[row2+1][col2+1] - integrogram[row2+1][col1] - integrogram[row1][col2+1] + integrogram[row1][col1];
    }
private:
    vector<vector<int>> integrogram;
    int n, m;
};


// Your NumMatrix object will be instantiated and called as such:
// NumMatrix numMatrix(matrix);
// numMatrix.sumRegion(0, 1, 2, 3);
// numMatrix.sumRegion(1, 2, 3, 4);

3. 1D, Mutable (一维，数据可变)

Given an integer array nums, find the sum of the elements between indices i and j (i ≤ j), inclusive.

The update(i, val) function modifies nums by updating the element at index i to val.
Example:
Given nums = [1, 3, 5]

sumRange(0, 2) -> 9
update(1, 2)
sumRange(0, 2) -> 8
Note:

  1. The array is only modifiable by the update function.
  2. You may assume the number of calls to update and sumRange function is distributed evenly.

Analysis

在Immutable的基础上，增加了update(index, value)， 即可以改变序列中任何位置的值。显然如果再使用刚才的算法，由于update的最大时间复杂度为O(n),因此整个算法的时间复杂度就增加到了O(n^2),因此需要一个复杂度更低的算法。可以从两方面入手update和query。需要将这两个函数的复杂度都降低到O(logn)以下(包括O(logn))。前面已经提到过需要*事先进行一些预处理，使得一些重复计算的东西不再重复计算，才能够将复杂度降低下来。

先预先计算一些区间的和值，然后把每个询问都拆成若干个计算了和的区间，并且将这些区间的和再相加，从而得出答案。这不就是线段树的思想吗？那就先从线段树说起。

线段树其实本质就是用一棵树来维护一段区间上和某个子区间相关的值——例如区间和、区间最大最小值一类的。它的具体做法是这样的，这棵树的根节点表示了整段区间，根节点的左儿子节点表示了这段区间的前半部分，根节点的右儿子节点表示了这段区间的后半部分——并以此类推，对于这棵树的每个节点，如果这个节点所表示的区间的长度大于1，则令其左儿子节点表示这段区间的前半部分，令其右儿子表示这段区间的后半部分。以一段长度为10的区间为例，所建立出的线段树应该是这样子的。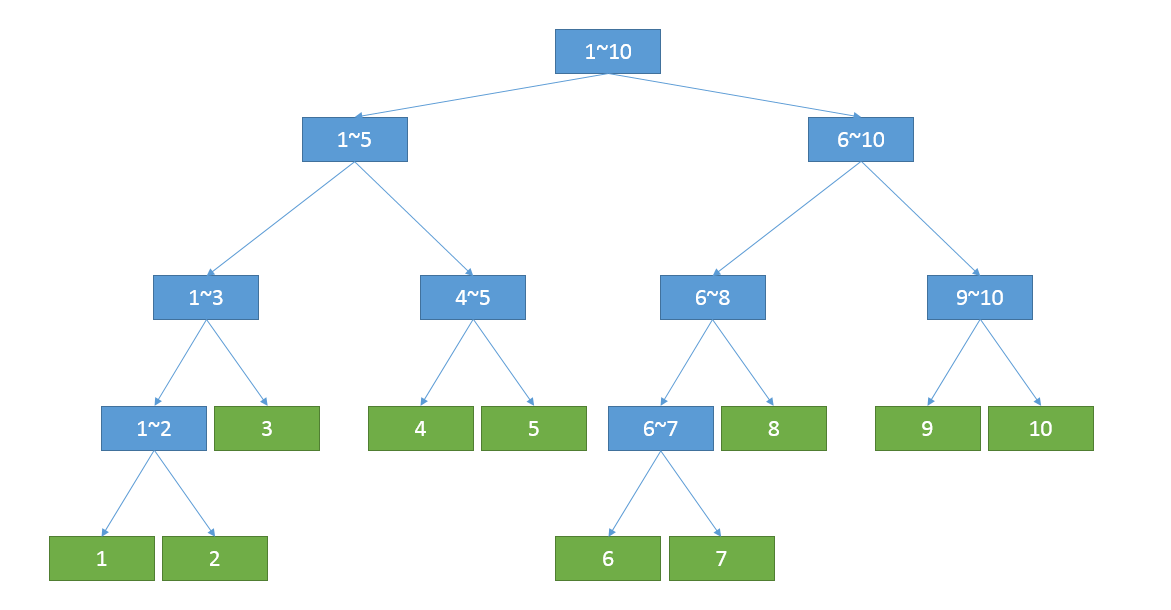
segment tree
就以RSQ(Range Sum Query)问题为例吧——RSQ问题要求的是求解一段区间中的和值，那么我不妨效仿ST算法，先对一些可能会用到的区间求解这个和值！而既然我要是用线段树来解决这个问题的，那么我不妨就将每一个节点对应的区间中的和值都求解出来。

那给定这样一组数据，将这个预处理的结果给我计算一下？
N=10
Weight = {3, 2, 9, 6, 7, 5, 4, 1, 8, 10}
这数据正好也只有10个位置，那么直接用这棵树了。由于每个非叶子节点所对应的区间都正好由它的两个儿子节点所对应的区间拼凑而成，这样一个节点所对应的区间中的和值便是它的两个儿子节点所对应的区间的和。这样我只需要O(N)的时间复杂度就可以计算出这棵树来。”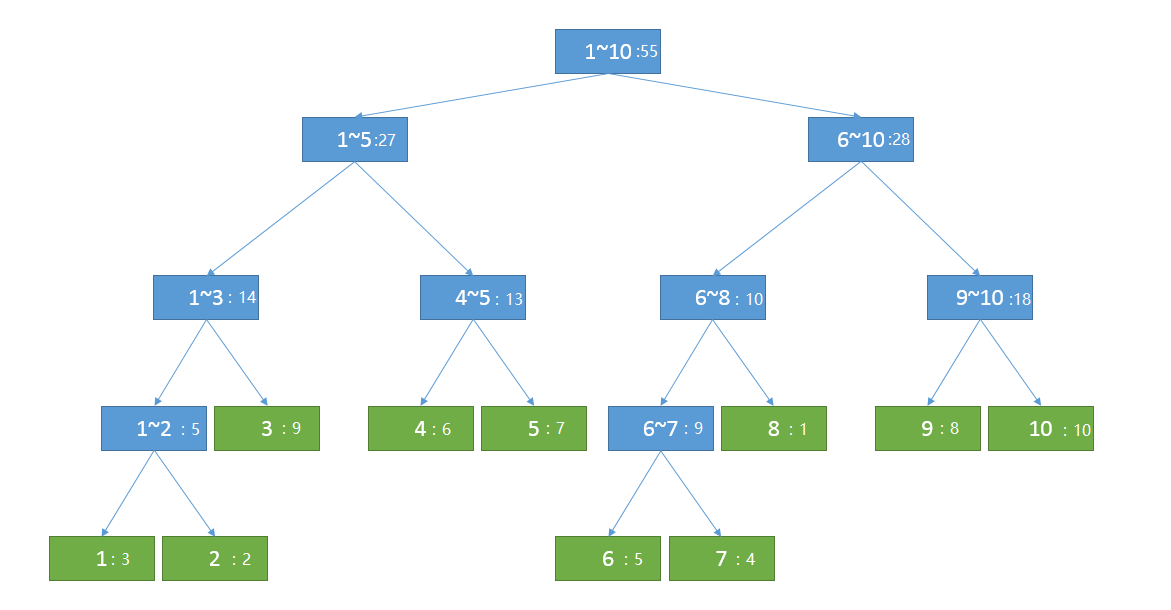

这样一棵树统计出来的区间怎样使用很快的算法进行查询？还有修改呢？”

先从简单的说起吧——修改，当某个位置的商品的重量发生改变的时候，对应的，就是这棵树的某个叶子节点的值发生了变化，包含这个节点的区间，便只有这个节点的所有祖先节点，而这样的节点数量事实上是很少的——只有O(log(N))级别。也就是说，当一次修改操作发生的时候，我只需要改变数量在O(log(N))级别的节点的值就可以完成操作了，修改的时间复杂度是O(log(N))。”

查询这个问题其实也不复杂！从线段树的根开始，对于当前访问的线段树节点t, 设其对应的区间为[A, B], 如果询问的区间[l, r]完全处于前半段或者后半段——即r <= (A + B)/2或者l > (A + B) / 2，那么递归进入t对应的子节点进行处理（因为另一棵子树中显然不会有任何区间需要用到）。否则的话，则把询问区间分成2部分[l, (A + B) / 2]和[(A + B) / 2 + 1, r]，并且分别进入t的左右子树处理这两段询问区间（因为2棵子树中显然都有区间需要用到）！当然了，如果[A, B]正好覆盖了[l, r]的话，就可以直接返回之前计算的t这棵子树中的和值了。还是之前那个例子，如果我要询问[3, 9]这段区间，我的最终结果会是这样的——橙色部分标注的区间。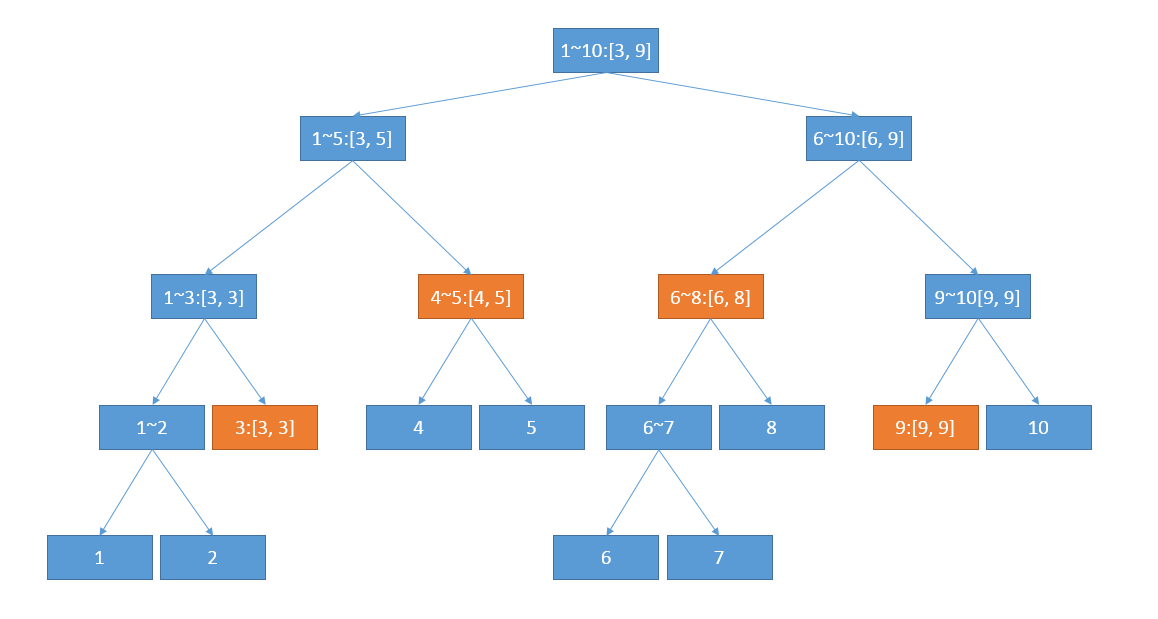

首先[3, 9]分解成了[3, 5]和[6, 9]两个区间，而[3, 5]分解成了[3, 3]和[4, 5]——均没有必要继续分解，[6, 9]分解成了[6, 8]和[9, 9]——同样也没有必要继续分解了。每一步的分解都是必要的，所以这已经是最好的分解方法了。”

但是这样分解的话，区间的个数能保证么？万一很多怎么办？其实不会的，除了第一次分解成2个区间的操作可能会将区间个数翻倍外，之后每一次分解的时候所处理的区间都肯定有一条边是和当前节点对应的重合的（即l=A或者r=B），也就是说即使再进行分解，分解出的两个区间中也一定会有一个区间是不需要再进行分解的，也就是区间的总数是在深度这个级别的，所以也是O(logN)的。

再总结一下，首先根据初始数据，使用O(N)的时间构建一棵最原始的线段树，这个过程中我会使用子节点的值来计算父亲节点的值，从而避免冗余计算。然后对于每一次操作，如果是一次修改的话，我就将修改的节点和这个节点的所有祖先节点的值都进行更新，可以用O(logN)的时间复杂度完成。而如果是一次询问的话，使用上面描述的方法来对询问区间进行分解，用O(logN)的时间复杂度完成。无论是修改还是查询的时间复杂度都是O(logN)的，所以我这个算法最终的时间复杂度会是O(N + Q * log(N))。

Cpp Code

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
class NumArray {
public:
    // 构建SegmentTree
    NumArray(vector<int> &nums) {
        n = nums.size();
        segmentTree.resize(n * 4 + 1);   // 4n的空间足够存储SegmentTree
        createTree(0, 0, n-1, nums);
    }
    // 修改
    void update(int i, int val) {
        update(0, 0, n-1, i, val);
    }
    // 查询
    int sumRange(int i, int j) {
        if(i < 0 || j > n-1)
            return 0;
        return query(0, 0, n-1, i, j);
    }
private:
    // 沿根结点向下查询
    int query(int node, int begin, int end, int i, int j)
    {
        if(begin == i && end == j)
            return segmentTree[node];
        int mid = (begin+end) >> 1;
        if(j <= mid)    // 位于左子树
            return query((node<<1)+1, begin, mid, i, j);
        else if(i > mid) // 位于右子树
            return query((node<<1)+2, mid+1, end, i, j);
        else  // 位于左子树和右子树
            return query((node<<1)+1, begin, mid, i, mid)
        + query((node<<1)+2, mid+1, end, mid+1, j);
    }
    // 沿着根结点向下更新，直到叶子结点
    void update(int node, int begin, int end, int id, int val)
    {
        if(id < begin || id > end)
            return;
        if(begin == end)
            segmentTree[node] = val;
        else
        {
            update((node<<1)+1, begin, (begin+end)>>1, id, val);
            update((node<<1)+2, ((begin+end)>>1)+1, end, id, val);
            segmentTree[node] = segmentTree[(node<<1)+1] + segmentTree[(node<<1)+2];
        }
    }
    // 创建SegmentTree
    void createTree(int node, int begin, int end, const vector<int>& nums)
    {
        if(end < begin)   // illegal
            return;
        if(begin == end) //叶子结点
            segmentTree[node] = nums[begin];
        else
        {
            // 递归构建左右子树
            createTree((node << 1)+1, begin, (begin+end)>>1, nums);
            createTree((node<<1)+2, ((begin+end)>>1)+1, end, nums);
            segmentTree[node] = segmentTree[(node<<1)+1] + segmentTree[(node<<1)+2];
        }
    }
private:
    vector<int> segmentTree;
    int n;
};

// Your NumArray object will be instantiated and called as such:
// NumArray numArray(nums);
// numArray.sumRange(0, 1);
// numArray.update(1, 10);
// numArray.sumRange(1, 2);

Summary
对于本题，有人提出了一种基于bucket的方法，更新和查询分别需要O(1)和O(n^0.5)时间复杂度的算法(more)如果将求和该为求最大或最小值，即变成了RMQ问题，同样的算法，只需修改几个地方，就不再赘述，对于RMQ，还有经典的ST算法。
另二维，数据可变的情况没有列出，读者可以自己思考。