题目描述
在一个整数序列中，统计每个元素其右边的元素中比本身小的元素个数，并返回。题目来源leetcode。
本题需要注意两点：元素均为整数，元素可能重复。
例子:
给定 nums = [5, 2, 6, 1]
- 5右边有两个更小的数 (2 , 1).
- 2右边有两个更小的数(1).
- 6右边有两个更小的数(1).
- 最右边的数没有比它小的数.
返回序列 count = [2, 1, 1, 0]。
思路
自右向左处理每一个数，我们知道对于每一个数，只要遍历它右边的每个数，再与本身做一个比较不就知道答案了吗？这样的算法不难想到，也容易实现，时间复杂度为O(n^2)。
这样的处理方法，对每个数的处理跟以前的都没有关系，比如这样的一个例子：
[7, 4, 5, 6, 2, 9, 8, 4, 7]
在处理9的时候，其实比9小的数就是9后边一个8对应的count加上8的个数。如果有这些信息我们很快就能得到9对应的count值。
在知道了处理的过程中是有信息可以利用的以后，在处理每个数的时候可以将复杂度降到O(logn)甚至O(k)，现在主要的任务是寻找一个适当的算法或数据结构。跟大小有关的数据结构我们知道有二叉搜索树，对每一个结点，左子树的值总是大于该结点的值，右子树的值总是小于该结点的值，左子树和右子树都是一棵二叉搜索树。
这样在处理的时候，实际上是在维护一棵二叉搜索树，二叉树每个结点，的数据结构和示意图如下：
1
2
3
4
5
6
7
8
| struct BinarySearchTreeNode
{
int val;
int less;
int count;
BinarySearchTreeNode *left, *right;
BinarySearchTreeNode(int value) : val(value), less(0),count(1),left(NULL), right(NULL) {}
};
|
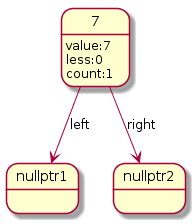
对上边的例子：
首先添加7作为根结点
对每一个数，ans初始化为0用来保存结果，从树根节点往下搜索，
- 当该数小于结点对应的数时，往右子树向下递归搜索，该结点的less加1
- 当该数大于结点对应的数时，往左子树向下递归搜索，ans加上该结点的count和less
- 当该数等于结点对应的数时，该结点的count加1，ans加上该结点的count
- 保存ans
返回ans每个数对应的ans
处理的过程伪代码如下：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
| // root为树的根结点
// node为一个结点
// ans表示最后的结果
insert(root, node, ans)
If node.value < root.value
root.less = root.less+1
If root.right is NULL
root.right <- node
return
End If
insert(root.right, node, ans)
Else If node.value > root.value
ans = ans + root.less + root.count
If root.left is NULL
root.left <- node
return
End If
insert(root.left, node, ans)
Else node.value == root.value
root.count = root.count + 1
ans = ans + root.less
End If
|
代码 Cpp
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
| // bianry search tree
struct BinarySearchTreeNode
{
int val;
int less;
int count;
BinarySearchTreeNode *left, *right;
BinarySearchTreeNode(int value) : val(value), less(0),count(1),left(NULL), right(NULL) {}
};
void insert(BinarySearchTreeNode *root, const int value, int &numLessThan)
{
if(value < root->val) // right
{
root->less++;
if(root->right == NULL)
root->right = new BinarySearchTreeNode(value);
else
insert(root->right, value, numLessThan);
}
else if(value > root->val)
{
numLessThan += root->less + root->count;
if(!root->left)
root->left = new BinarySearchTreeNode(value);
else
insert(root->left, value, numLessThan);
}
else
{
numLessThan += root->less;
root->count++;
}
}
vector<int> countSmaller(vector<int>& nums) {
vector<int> count(nums.size());
if(nums.size() == 0)
return count;
BinarySearchTreeNode root(nums[nums.size()-1]);
for(int i = nums.size() - 2; i >= 0; i--)
{
int numLessThan = 0;
insert(&root, nums[i], numLessThan);
count[i] = numLessThan;
}
return count;
}
// int arr[] = {7, 4, 5, 6, 2, 9, 8, 4, 7}
// vector<int> nums(begin(arr), end(arr));
// auto vec = countSmaller(nums);
// for(auto x : vex)
// cout << x << " ";
// input: [7, 4, 5, 6, 2, 9, 8, 4, 7]
// output: [5, 1, 2, 2, 0, 3, 2, 0, 0]
|
运算过程
下面是该例子的处理过程中的示意图：
![[8,4,7]](/images/binary_search_tree_half.png)
最后该二叉搜索树如下：
![final binary search tree of [7, 4, 5, 6, 2, 9, 8, 4, 7]](/images/binary_search_tree.png)
总结
虽然该算法的平均复杂度还能达到O(logn)，但在最坏的情况下为O(n^2)。原因是二叉搜索树退化成了一个链表。比如一个非递减序列或一个非递增序列。
该方法还有其他的解法，诸如像segment-tree、binary-indexed-tree、divide-and-conquer等方法。
